Visualizing Satellite Beam Coverage

A Guide to Understanding Signal Models Using Python

How Satellites Create Coverage Patterns On Earth Using Conic Geometry

Satellites are a cornerstone of modern communication, enabling everything from global broadcasting to providing internet connectivity in remote areas. To effectively design, manage, and optimize these sophisticated communication links, engineers rely on satellite beam models. These models are essential for visualizing how a satellite's signal, often shaped like a cone, projects onto the Earth's surface to cover specific geographic areas.

The shape of this coverage area is a direct result of conic geometry. When a satellite's cone-shaped transmission beam intersects with the (approximately) spherical Earth, the footprint on the ground is an ellipse. Understanding this geometric relationship is important for predicting and optimizing signal distribution.

In this post, we'll walk through a code example that models a satellite beam, breaking down the calculations and visualizations along the way.

Libraries

Let's look at what each library brings to the project:

import numpy as np
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import cartopy.feature as cfeature

• NumPy (np): NumPy allows us to work with arrays (like grids of coordinates or signal strengths) and perform mathematical operations.

• Matplotlib (plt): A library for creating visualizations. We'll use it for plotting satellite beam coverage on a map.

• Cartopy (ccrs, cfeature): A library for geospatial data processing and map creation, integrating with Matplotlib.

Defining Earth's Radius

Many of the calculations will involve the Earth's geometry. While the Earth isn't a perfect sphere, using an average radius is a common and effective approximation for many satellite modeling applications.

R_e: float = 6371.0  # Average Earth's radius in kilometers

• R_e: This variable stores the average radius of the Earth in kilometers. It's a constant that will be used in the function to convert geographic coordinates (latitude, longitude) into a 3D Cartesian system, which is suitable for spatial calculations.

Transforming Coordinates From Geographic to ECEF

To accurately model the satellite's position and how its beam interacts with Earth, we need a consistent coordinate system. We often think of locations in terms of latitude, longitude, and altitude (geodetic coordinates), but 3D spatial calculations are more straightforward in a Cartesian system. Therefore, we'll use the Earth-Centered, Earth-Fixed (ECEF) system, which is a Cartesian coordinate system where the origin (0,0,0) is at the Earth's center, the X-axis points towards the intersection of the Prime Meridian and the Equator, the Z-axis points towards the North Pole, and the Y-axis completes a right-handed system.

The geodetic_to_ecef function handles this conversion:

def geodetic_to_ecef(lat: float, lon: float, alt: float) -> np.ndarray:
    """
    Convert geodetic coordinates (latitude, longitude, altitude) to 
    Earth-Centered, Earth-Fixed (ECEF) Cartesian coordinates.
    Assumes a spherical Earth model using R_e.
    """
    lat_rad = np.radians(lat)  # Convert latitude to radians
    lon_rad = np.radians(lon)  # Convert longitude to radians
    
    # Calculate ECEF coordinates
    x = (R_e + alt) * np.cos(lat_rad) * np.cos(lon_rad)
    y = (R_e + alt) * np.cos(lat_rad) * np.sin(lon_rad)
    z = (R_e + alt) * np.sin(lat_rad)  # Note: Uses R_e + alt for z as well
    
    return np.array([x, y, z])

• Purpose: This function takes a point's latitude, longitude, and altitude (relative to the spherical Earth model) and converts it into [x, y, z] ECEF coordinates. This transformation is important for calculating distances and angles in 3D space between the satellite, points on Earth, and the beam itself.

• Process:

  1. Converts lat and lon from degrees to radians, as trigonometric functions in NumPy expect radians.

  2. Applies standard spherical-to-Cartesian conversion formulas, incorporating the altitude (alt) with Earth's radius (R_e) to determine the distance from the Earth's center to the point.

Calculating Signal Strength

EIRP, or Effective Isotropic Radiated Power, indicates the power density of the satellite's signal at a given point on Earth. A higher EIRP generally means a stronger, better quality signal. This function will calculate EIRP values across a grid of points on the Earth's surface.

def calculate_eirp(
    lat_grid: np.ndarray, 
    lon_grid: np.ndarray, 
    sat_pos_ecef: np.ndarray, 
    beam_dir_ecef: np.ndarray, 
    beam_half_angle_rad: float, 
    max_eirp: float, 
    sat_altitude: float
) -> np.ndarray:
    # Convert grid points (on Earth's surface, so alt=0) to ECEF
    lat_rad_grid = np.radians(lat_grid)
    lon_rad_grid = np.radians(lon_grid)
    
    x_points = R_e * np.cos(lat_rad_grid) * np.cos(lon_rad_grid)
    y_points = R_e * np.cos(lat_rad_grid) * np.sin(lon_rad_grid)
    z_points = R_e * np.sin(lat_rad_grid)
    points_ecef = np.stack((x_points, y_points, z_points), axis=-1)

    # Visibility Check (Line-of-sight from satellite to Earth points)
    vec_earth_center_to_sat = sat_pos_ecef 
    dot_product = points_ecef @ vec_earth_center_to_sat 
    norm_points_ecef = np.linalg.norm(points_ecef, axis=-1) 
    norm_sat_pos_ecef = np.linalg.norm(sat_pos_ecef)       
    cos_beta = dot_product / (norm_points_ecef * norm_sat_pos_ecef)
    cos_theta_max = R_e / (R_e + sat_altitude) # Cosine of angle to horizon from sat
    visible_mask = cos_beta >= cos_theta_max

    # Beam Angle Calculation
    vec_sat_to_point = points_ecef - sat_pos_ecef 
    norm_vec_sat_to_point = np.linalg.norm(vec_sat_to_point, axis=-1, keepdims=True)
    safe_norm_vec_sat_to_point = np.where(norm_vec_sat_to_point == 0, 1e-9, norm_vec_sat_to_point)
    vec_sat_to_point_normalized = vec_sat_to_point / safe_norm_vec_sat_to_point
    beam_dir_normalized = beam_dir_ecef / np.linalg.norm(beam_dir_ecef)
    
    # Cosine of the angle between beam's boresight and vector to each point
    cos_angle_from_boresight = np.einsum('ijk,k->ij', vec_sat_to_point_normalized, beam_dir_normalized)
    cos_angle_from_boresight = np.clip(cos_angle_from_boresight, -1.0, 1.0) # Avoid domain errors
    angle_from_boresight_rad = np.arccos(cos_angle_from_boresight)

    # EIRP Calculation using Gaussian Beam Model
    within_beam_mask = np.logical_and(angle_from_boresight_rad <= beam_half_angle_rad, visible_mask)
    
    # sigma for Gaussian model where beam_half_angle_rad is the angle for -3dB fall-off (half-power point)
    sigma_for_gaussian = beam_half_angle_rad / np.sqrt(2 * np.log(2)) 
    if beam_half_angle_rad == 0: sigma_for_gaussian = 1e-9 # Avoid division by zero for pencil beam
    
    eirp = np.zeros_like(lat_grid, dtype=float) 
    if beam_half_angle_rad > 0:
        exponent_term = - (angle_from_boresight_rad[within_beam_mask]**2) / (2 * sigma_for_gaussian**2)
        eirp[within_beam_mask] = max_eirp * np.exp(exponent_term)
    elif beam_half_angle_rad == 0: # Pencil beam
        pencil_beam_points = np.logical_and(within_beam_mask, np.isclose(angle_from_boresight_rad, 0))
        eirp[pencil_beam_points] = max_eirp
        
    return eirp

• Purpose: This function determines how the satellite's signal strength (EIRP) is distributed across the Earth's surface, considering the satellite's position, beam direction, and beam shape.

• Process:

  1. Coordinate Conversion: Converts each latitude/longitude point in the input grid (lat_grid, lon_grid) to ECEF coordinates. These points are assumed to be on the Earth's surface (altitude = 0).

  2. Visibility Check: Determines if each grid point is actually visible (has line-of-sight) from the satellite. A point is visible if the angle between the vector from Earth's center to the satellite and the vector from Earth's center to the point is less than the angle to the Earth's horizon as seen from the satellite.

  3. Beam Angle Calculation: For each visible grid point, it calculates the angle between:

     • The satellite beam's main direction (boresight).

     • The vector pointing from the satellite to that grid point. The np.einsum function is used here for an efficient "batched" dot product to calculate the cosine of this angle across all grid points simultaneously.

  4. Gaussian Beam Model: It then applies a Gaussian model to simulate how signal strength typically decreases as you move away from the beam's center.

     • Points are considered "within the beam" if their calculated angle from the boresight is less than or equal to the defined beam_half_angle_rad and they are visible.

     • The sigma parameter in the Gaussian formula (e−angle2/(2σ2)) defines the "spread" of the beam. We calculate it based on beam_half_angle_rad, assuming this half-angle corresponds to the point where the power drops by 3dB (half its maximum value).

     • Only points falling within this defined beam cone and visible to the satellite will have a non-zero EIRP.

Setting Satellite and Beam Parameters

To model a specific scenario, we need to define key parameters for the satellite and its transmission beam.

# Satellite Parameters
sat_altitude_km: float = 35786.0  # Altitude for a geostationary orbit (km)
sat_lat_deg: float = 0.0          # Latitude for GEO (0° for equator)
sat_lon_deg: float = 90.0         # Example satellite longitude (degrees East)

# Beam Parameters
beam_center_lat_deg: float = 0.0  # Target latitude for the beam's center
beam_center_lon_deg: float = 0.0  # Target longitude for the beam's center
beam_width_deg: float = 5.0       # Full angular width of the beam (degrees)
max_eirp_dbw: float = 50.0        # Maximum EIRP at the beam's center (dBW)

# Derived beam parameter
beam_half_angle_deg = beam_width_deg / 2.0
beam_half_angle_rad = np.radians(beam_half_angle_deg)

• Geostationary Orbit: An altitude of approximately 35,786 km above the equator means the satellite orbits at the same speed as the Earth's rotation, appearing stationary from the ground. This is ideal for continuous coverage of a specific region.

• Beam Width: This defines the angular spread of the satellite's signal. A narrower beam concentrates power over a smaller area (higher EIRP, smaller footprint), while a wider beam covers a larger area (lower EIRP, larger footprint). We use beam_half_angle_rad (half of the full width, in radians) in our calculations.

Determining Satellite and Beam Position in 3D Space

With these parameters defined, we convert the satellite's location and the beam's target center on Earth into the ECEF coordinate system. We also determine the beam's direction vector.

sat_pos_ecef = geodetic_to_ecef(sat_lat_deg, sat_lon_deg, sat_altitude_km)
beam_center_on_earth_ecef = geodetic_to_ecef(beam_center_lat_deg, beam_center_lon_deg, 0) # Altitude is 0 for Earth surface
beam_dir_ecef = beam_center_on_earth_ecef - sat_pos_ecef

• Purpose: These ECEF coordinates and the direction vector precisely define the geometry in our scenario in 3D space. sat_pos_ecef is the satellite's location, and beam_dir_ecef is a vector pointing from the satellite towards the intended center of its coverage area on the Earth's surface.

Creating the Grid for Evaluating Coverage

To visualize the beam's coverage, we need to calculate the EIRP at many different points on the Earth using a grid of latitude and longitude points.

lats_deg = np.linspace(-90, 90, 361)  # Grid points from South Pole to North Pole (e.g., every 0.5 degrees)
lons_deg = np.linspace(-180, 180, 721) # Grid points around the globe (e.g., every 0.5 degrees)
lon_grid_deg, lat_grid_deg = np.meshgrid(lons_deg, lats_deg)

• Purpose: np.linspace creates evenly spaced arrays of latitude and longitude values. np.meshgrid then takes these 1D arrays and creates two 2D arrays (lon_grid_deg and lat_grid_deg). These 2D arrays define the coordinates of every point in our evaluation grid, covering the entire globe (or a specified region). The resolution (number of points, e.g., 361x721) determines the detail of our final plot.

Calculating and Optionally Filtering EIRP Values

Now, we apply the calculate_eirp function to every point on the grid. This generates a 2D array of EIRP values, corresponding to the lat/lon grid.

eirp_values = calculate_eirp(
    lat_grid_deg, lon_grid_deg, 
    sat_pos_ecef, beam_dir_ecef, 
    beam_half_angle_rad, max_eirp_dbw, sat_altitude_km
)

# For plotting, we might want to treat very low or zero EIRP values as "no signal"
# This can be done by masking these values (e.g., making them transparent in the plot)
# eirp_plot_values = np.ma.masked_where(eirp_values < 0.1, eirp_values) 

• Purpose: This step generates the raw data for the visualization. The eirp_values array holds the calculated signal strength at each point on the global grid. Filtering or masking low values (as shown in the commented line) can help make the plot cleaner by showing only areas with significant signal.

Visualizing the Results

The final step is to display the calculated EIRP data on a world map. We'll use Matplotlib and Cartopy to create an orthographic (globe-like) projection.

fig = plt.figure(figsize=(12, 10))

# Define the map projection (Orthographic for a globe view)
# Center the projection on the beam's target area for better focus
projection_center_lon = beam_center_lon_deg
projection_center_lat = beam_center_lat_deg
ax = plt.axes(projection=ccrs.Orthographic(
    central_longitude=projection_center_lon,
    central_latitude=projection_center_lat
))

# Add geographical features to the map
ax.add_feature(cfeature.OCEAN, zorder=0, facecolor='lightblue', alpha=0.7)
ax.add_feature(cfeature.LAND, zorder=0, edgecolor='black', facecolor='lightgreen', alpha=0.5)
ax.add_feature(cfeature.COASTLINE, zorder=1, linewidth=0.8)
ax.add_feature(cfeature.BORDERS, zorder=1, linestyle=':', linewidth=0.6)
ax.gridlines(crs=ccrs.PlateCarree(), draw_labels=False,
             linewidth=0.5, color='gray', alpha=0.5, linestyle='--')

# Mask low EIRP values for cleaner plotting
eirp_plot_values = np.ma.masked_where(eirp_values < 0.1, eirp_values) 

# Plot the EIRP data using pcolormesh for a continuous representation
# The 'transform=ccrs.PlateCarree()' tells Cartopy the data grid is in standard lat/lon
img = ax.pcolormesh(
    lon_grid_deg, lat_grid_deg, eirp_plot_values,
    transform=ccrs.PlateCarree(),
    cmap='viridis',  # Colormap for signal strength
    shading='auto'   # Adjusts shading; 'gouraud' can be smoother
)

# Add a colorbar to show the EIRP scale
cbar = plt.colorbar(img, ax=ax, orientation='vertical', pad=0.05, shrink=0.7)
cbar.set_label(f'EIRP ({max_eirp_dbw:.0f} dBW Peak Scale)')

# Add a title with key parameters
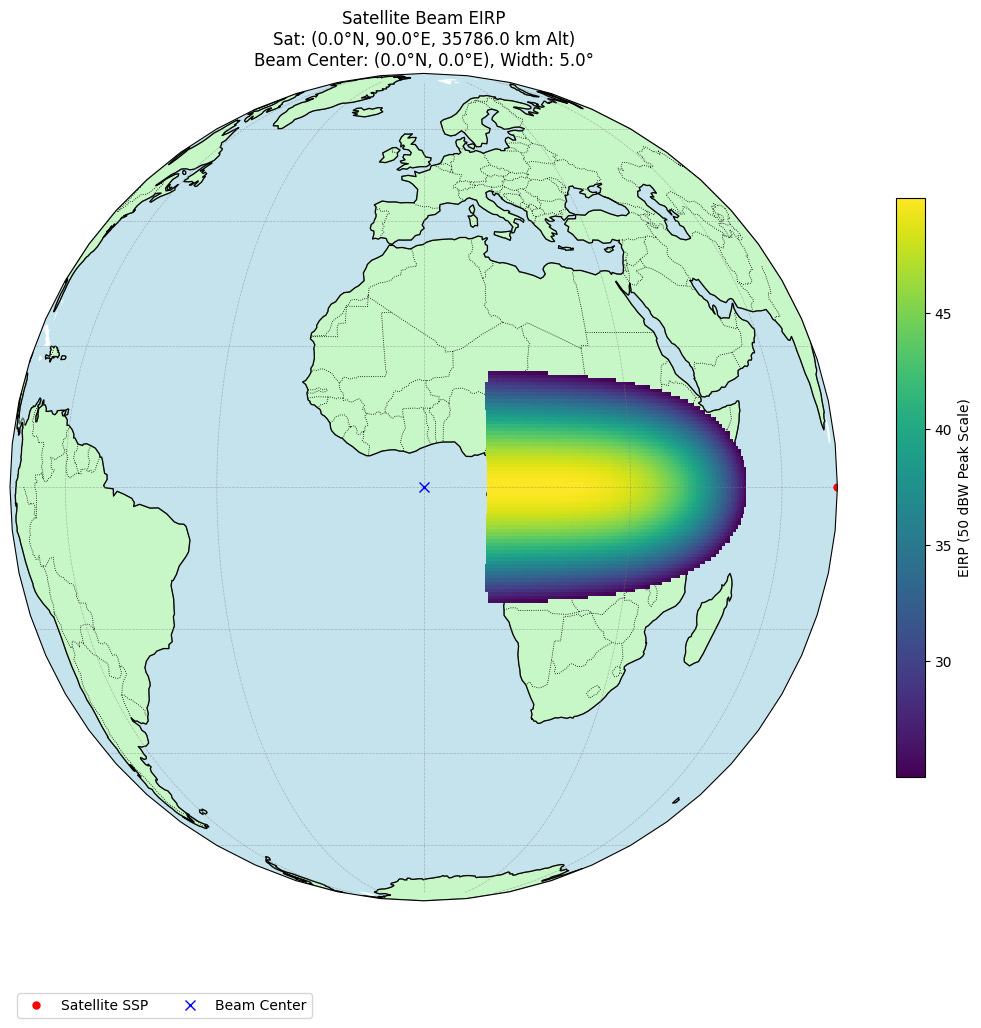
plt.title(
    f'Satellite Beam EIRP\nSat: ({sat_lat_deg}°N, {sat_lon_deg}°E, {sat_altitude_km} km Alt)\n'
    f'Beam Center: ({beam_center_lat_deg}°N, {beam_center_lon_deg}°E), Width: {beam_width_deg}°',
    fontsize=12
)

# Optionally, mark satellite sub-point and beam center
ax.plot(sat_lon_deg, sat_lat_deg, 'ro', markersize=5, transform=ccrs.Geodetic(), label='Satellite SSP')
ax.plot(beam_center_lon_deg, beam_center_lat_deg, 'bx', markersize=7, transform=ccrs.Geodetic(), label='Beam Center')
ax.legend(loc='lower left', bbox_to_anchor=(0.0, -0.15), ncol=2)

plt.tight_layout() # Adjust plot for a tight layout
plt.show()

• Cartopy Setup: We initialize a Matplotlib figure and an axes object with a specific Cartopy projection (ccrs.Orthographic). Centering this projection on the beam's target helps to best display the coverage area.

• Adding Features: cfeature is used to draw oceans, landmasses, coastlines, and country borders, providing geographical context.

• Plotting Data: ax.pcolormesh is good for displaying 2D gridded data like the EIRP values. It creates a colored representation where each cell in the grid is colored according to its EIRP. The transform=ccrs.PlateCarree() argument tells Cartopy that the lon_grid_deg and lat_grid_deg arrays represent standard geographic coordinates.

• Colormap and Colorbar: A colormap (e.g., 'viridis') visually translates EIRP values into colors, and a colorbar provides a legend for these colors.

• Title and Labels: Clear titles and labels make the plot understandable.

• Display: Finally, plt.show() displays the generated map.

This visualization effectively shows where the satellite's signal is strongest and how it diminishes across the coverage footprint.

Conclusion

This article demonstrated the application of conic geometry principles to model satellite beam coverage on the Earth's surface. The framework, employing coordinate transformations and a Gaussian beam model, illustrated the distribution of Effective Isotropic Radiated Power (EIRP). These types of models are fundamental for the design, optimization, and performance prediction of satellite communication systems.

Appendix

To make the code more convenient and flexible, we can encapsulate the main logic into a function that accepts input parameters. This will allow you to easily change the satellite and beam parameters without modifying the core code. Here's the full code used in the post:

import numpy as np
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import cartopy.feature as cfeature # For map features like land, ocean, borders

# --- Constants ---
R_e: float = 6371.0  # Earth's radius in km

# --- Coordinate Transformation ---
def geodetic_to_ecef(lat: float, lon: float, alt: float) -> np.ndarray:
    """
    Convert geodetic coordinates (latitude, longitude, altitude) to 
    Earth-Centered, Earth-Fixed (ECEF) Cartesian coordinates.

    Args:
        lat (float): Latitude in degrees.
        lon (float): Longitude in degrees.
        alt (float): Altitude in kilometers above the Earth's surface.

    Returns:
        np.ndarray: ECEF coordinates as a numpy array [x, y, z].
    """
    lat_rad = np.radians(lat)
    lon_rad = np.radians(lon)
    
    # Calculate ECEF coordinates
    x = (R_e + alt) * np.cos(lat_rad) * np.cos(lon_rad)
    y = (R_e + alt) * np.cos(lat_rad) * np.sin(lon_rad)
    z = (R_e + alt) * np.sin(lat_rad)
    
    return np.array([x, y, z])

# --- EIRP Calculation ---
def calculate_eirp(
    lat_grid: np.ndarray, 
    lon_grid: np.ndarray, 
    sat_pos_ecef: np.ndarray, 
    beam_dir_ecef: np.ndarray, 
    beam_half_angle_rad: float, 
    max_eirp: float, 
    sat_altitude: float
) -> np.ndarray:
    """
    Calculate the Effective Isotropic Radiated Power (EIRP) for each point on a grid.

    Args:
        lat_grid (np.ndarray): Grid of latitudes (degrees).
        lon_grid (np.ndarray): Grid of longitudes (degrees).
        sat_pos_ecef (np.ndarray): Satellite position in ECEF coordinates [x, y, z] (km).
        beam_dir_ecef (np.ndarray): Beam direction vector in ECEF coordinates [x, y, z].
        beam_half_angle_rad (float): Half-angle of the beam in radians.
        max_eirp (float): Maximum EIRP (e.g., in dBW).
        sat_altitude (float): Satellite altitude in kilometers.

    Returns:
        np.ndarray: EIRP values for each point on the grid.
    """
    # Convert grid points (on Earth's surface, so alt=0) to ECEF
    lat_rad_grid = np.radians(lat_grid)
    lon_rad_grid = np.radians(lon_grid)
    
    x_points = R_e * np.cos(lat_rad_grid) * np.cos(lon_rad_grid)
    y_points = R_e * np.cos(lat_rad_grid) * np.sin(lon_rad_grid)
    z_points = R_e * np.sin(lat_rad_grid)
    points_ecef = np.stack((x_points, y_points, z_points), axis=-1) # Shape: (n_lats, n_lons, 3)

    # --- Visibility Check (Line-of-sight from satellite to Earth points) ---
    vec_earth_center_to_sat = sat_pos_ecef 
    dot_product = points_ecef @ vec_earth_center_to_sat 

    norm_points_ecef = np.linalg.norm(points_ecef, axis=-1) 
    norm_sat_pos_ecef = np.linalg.norm(sat_pos_ecef)       
    
    cos_beta = dot_product / (norm_points_ecef * norm_sat_pos_ecef)
    cos_theta_max = R_e / (R_e + sat_altitude)
    visible_mask = cos_beta >= cos_theta_max

    # --- Beam Angle Calculation ---
    vec_sat_to_point = points_ecef - sat_pos_ecef 
    norm_vec_sat_to_point = np.linalg.norm(vec_sat_to_point, axis=-1, keepdims=True)
    safe_norm_vec_sat_to_point = np.where(norm_vec_sat_to_point == 0, 1e-9, norm_vec_sat_to_point)
    vec_sat_to_point_normalized = vec_sat_to_point / safe_norm_vec_sat_to_point

    beam_dir_normalized = beam_dir_ecef / np.linalg.norm(beam_dir_ecef)
    cos_angle_from_boresight = np.einsum('ijk,k->ij', vec_sat_to_point_normalized, beam_dir_normalized)
    cos_angle_from_boresight = np.clip(cos_angle_from_boresight, -1.0, 1.0)
    angle_from_boresight_rad = np.arccos(cos_angle_from_boresight)

    # --- EIRP Calculation using Gaussian Beam Model ---
    within_beam_mask = np.logical_and(angle_from_boresight_rad <= beam_half_angle_rad, visible_mask)
    
    # sigma for Gaussian model where beam_half_angle_rad is the angle for -3dB fall-off (half-power point)
    sigma_for_gaussian = beam_half_angle_rad / np.sqrt(2 * np.log(2)) 
    # Handle cases where beam_half_angle_rad is zero to avoid division by zero in sigma or exponent
    if beam_half_angle_rad == 0: # Pencil beam, only max EIRP at the exact boresight if within_beam
        sigma_for_gaussian = 1e-9 # A very small sigma, effectively a delta function
    
    eirp = np.zeros_like(lat_grid, dtype=float) 
    
    # Calculate EIRP for points within the beam using the Gaussian model
    if beam_half_angle_rad > 0: # Avoid division by zero if beam_half_angle is 0
        exponent_term = - (angle_from_boresight_rad[within_beam_mask]**2) / (2 * sigma_for_gaussian**2)
        eirp[within_beam_mask] = max_eirp * np.exp(exponent_term)
    elif beam_half_angle_rad == 0: # Pencil beam case
        # For a true pencil beam, only the exact center (angle=0) gets max_eirp
        # This is tricky with discrete grids. We can assign max_eirp if angle is very close to 0.
        pencil_beam_points = np.logical_and(within_beam_mask, np.isclose(angle_from_boresight_rad, 0))
        eirp[pencil_beam_points] = max_eirp
        
    return eirp

# --- Plotting Function ---
def plot_satellite_beam_cartopy(
    sat_altitude_km: float, 
    sat_lat_deg: float, 
    sat_lon_deg: float, 
    beam_center_lat_deg: float, 
    beam_center_lon_deg: float, 
    beam_width_deg: float, 
    max_eirp_val: float
) -> None:
    """
    Calculates and plots the satellite beam coverage on a map using Cartopy.

    Args:
        sat_altitude_km (float): Satellite altitude in kilometers.
        sat_lat_deg (float): Satellite latitude in degrees.
        sat_lon_deg (float): Satellite longitude in degrees.
        beam_center_lat_deg (float): Beam center latitude in degrees.
        beam_center_lon_deg (float): Beam center longitude in degrees.
        beam_width_deg (float): Full beam width in degrees.
        max_eirp_val (float): Maximum EIRP (e.g., in dBW).
    """
    beam_half_angle_deg = beam_width_deg / 2.0
    beam_half_angle_rad = np.radians(beam_half_angle_deg)

    sat_pos_ecef = geodetic_to_ecef(sat_lat_deg, sat_lon_deg, sat_altitude_km)
    beam_center_on_earth_ecef = geodetic_to_ecef(beam_center_lat_deg, beam_center_lon_deg, 0)
    beam_dir_ecef = beam_center_on_earth_ecef - sat_pos_ecef

    lats_deg = np.linspace(-90, 90, 361)  # Grid resolution
    lons_deg = np.linspace(-180, 180, 721) 
    lon_grid_deg, lat_grid_deg = np.meshgrid(lons_deg, lats_deg)

    eirp_values = calculate_eirp(
        lat_grid_deg, lon_grid_deg, 
        sat_pos_ecef, beam_dir_ecef, 
        beam_half_angle_rad, max_eirp_val, sat_altitude_km
    )

    fig = plt.figure(figsize=(12, 10))
    
    # Center projection on beam or satellite location. For these params, (0,0) is fine.
    # If sat_lon = 90 and beam_center_lon = 0, the beam is significantly off-nadir.
    # Centering on beam_center_lon makes more sense to see the beam shape clearly.
    projection_center_lon = beam_center_lon_deg
    projection_center_lat = beam_center_lat_deg
    
    ax = plt.axes(projection=ccrs.Orthographic(
        central_longitude=projection_center_lon,
        central_latitude=projection_center_lat
    ))

    ax.add_feature(cfeature.OCEAN, zorder=0, facecolor='lightblue', alpha=0.7)
    ax.add_feature(cfeature.LAND, zorder=0, edgecolor='black', facecolor='lightgreen', alpha=0.5)
    ax.add_feature(cfeature.COASTLINE, zorder=1, linewidth=0.8)
    ax.add_feature(cfeature.BORDERS, zorder=1, linestyle=':', linewidth=0.6)
    ax.gridlines(crs=ccrs.PlateCarree(), draw_labels=False,
                 linewidth=0.5, color='gray', alpha=0.5, linestyle='--')

    eirp_plot_values = np.ma.masked_where(eirp_values < 0.1, eirp_values) 

    img = ax.pcolormesh(
        lon_grid_deg, lat_grid_deg, eirp_plot_values,
        transform=ccrs.PlateCarree(),
        cmap='viridis', 
        shading='auto' 
    )

    cbar = plt.colorbar(img, ax=ax, orientation='vertical', pad=0.05, shrink=0.7)
    cbar.set_label(f'EIRP ({max_eirp_val:.0f} dBW Peak Scale)')

    plt.title(
        f'Satellite Beam EIRP\nSat: ({sat_lat_deg}°N, {sat_lon_deg}°E, {sat_altitude_km} km Alt)\n'
        f'Beam Center: ({beam_center_lat_deg}°N, {beam_center_lon_deg}°E), Width: {beam_width_deg}°',
        fontsize=12
    )
    
    ax.plot(sat_lon_deg, sat_lat_deg, 'ro', markersize=5, transform=ccrs.Geodetic(), label='Satellite SSP')
    ax.plot(beam_center_lon_deg, beam_center_lat_deg, 'bx', markersize=7, transform=ccrs.Geodetic(), label='Beam Center')
    
    # Adjust legend position to avoid overlap if projection center is (0,0) and beam is there.
    # For sat_lon=90, beam_lon=0, the default legend position should be fine.
    ax.legend(loc='lower left', bbox_to_anchor=(0.0, -0.15), ncol=2)


    plt.tight_layout()
    plt.show()

# --- Example Usage ---
if __name__ == '__main__':
    # Parameters from the original article
    satellite_altitude_km: float = 35786.0  # km (Geostationary orbit)
    satellite_latitude_deg: float = 0.0     # Geostationary satellites are over the equator
    satellite_longitude_deg: float = 90.0   # Satellite longitude (degrees East)
    
    beam_target_latitude_deg: float = 0.0   # Beam center latitude (degrees)
    beam_target_longitude_deg: float = 0.0  # Beam center longitude (degrees East)
    
    beam_angular_width_deg: float = 5.0     # Degrees (Full beamwidth)
    max_eirp_dbw: float = 50.0              # dBW

    print("Plotting with original article settings...")
    plot_satellite_beam_cartopy(
        sat_altitude_km=satellite_altitude_km,
        sat_lat_deg=satellite_latitude_deg,
        sat_lon_deg=satellite_longitude_deg,
        beam_center_lat_deg=beam_target_latitude_deg,
        beam_center_lon_deg=beam_target_longitude_deg,
        beam_width_deg=beam_angular_width_deg,
        max_eirp_val=max_eirp_dbw
    )